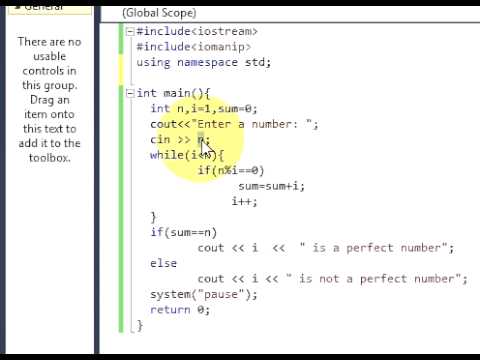
Amicable Numbers Program
Bell number Wikipedia. In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 1. Japan, but they are named after Eric Temple Bell, who wrote about them in the 1. Starting with B0 B1 1, the first few Bell numbers are 1, 1, 2, 5, 1. A0. 00. 11. 0 in the OEIS. Lego Super Marvel Heroes here. The nth of these numbers, Bn, counts the number of different ways to partition a set that has exactly n elements, or equivalently, the number of equivalence relations on it. Various Number Theorists Home PagesDepartmental listings Complete listing A B C D E F G H I J K L M N O P Q R S T U V. TeachWithMovies. org Create Lesson Plans from 425 Movies and Film Clips, Contact, Space Travel, Science Fiction. Mr. author infact 1,2,3,4,5,6,7,8,9 is also an armstrong number but your program doesnt display those so plz do the necessary. Outside of mathematics, the same number also counts the number of different rhyme schemes for n line poems. As well as appearing in counting problems, these numbers have a different interpretation, as moments of probability distributions. In particular, Bn is the nth moment of a Poisson distribution with mean 1. CountingeditSet partitionsedit. Partitions of sets can be arranged in a partial order, showing that each partition of a set of size n uses one of the partitions of a set of size n 1. The 5. 2 partitions of a set with 5 elements. In general, Bn is the number of partitions of a set of size n. A partition of a set S is defined as a set of nonempty, pairwise disjoint subsets of S whose union is S. For example, B3 5 because the 3 element set a, b, c can be partitioned in 5 distinct ways a, b, c a, b, c b, a, c c, a, b a, b, c. B0 is 1 because there is exactly one partition of the empty set. Every member of the empty set is a nonempty set that is vacuously true, and their union is the empty set. Therefore, the empty set is the only partition of itself. As suggested by the set notation above, we consider neither the order of the partitions nor the order of elements within each partition. This means that the following partitionings are all considered identical b, a, c a, c, b b, c, a c, a, b. If, instead, different orderings of the sets are considered to be different partitions, then the number of these ordered partitions is given by the ordered Bell numbers. FactorizationseditIf a number N is a squarefree positive integer meaning that it is the product of some number n of distinct prime numbers, then Bn gives the number of different multiplicative partitions of N. Amicable Numbers Program' title='Amicable Numbers Program' />These are factorizations of N into numbers greater than one, treating two factorizations as the same if they have the same factors in a different order. For instance, 3. B3 5 factorizations 3. A software platform for distributed computing using volunteer computer resources. Descriptions of areascourses in number theory. Mathematics Subject Classification, 11XX Eric Weissteins World of Mathematics Number Theory section. Rhyme schemeseditThe Bell numbers also count the rhyme schemes of an n line poem or stanza. A rhyme scheme describes which lines rhyme with each other, and so may be interpreted as a partition of the set of lines into rhyming subsets. Rhyme schemes are usually written as a sequence of Roman letters, one per line, with rhyming lines given the same letter as each other, and with the first lines in each rhyming set labeled in alphabetical order. Thus, the 1. 5 possible four line rhyme schemes are AAAA, AAAB, AABA, AABB, AABC, ABAA, ABAB, ABAC, ABBA, ABBB, ABBC, ABCA, ABCB, ABCC, and ABCD. PermutationseditThe Bell numbers come up in a card shuffling problem mentioned in the addendum to Gardner 1. If a deck of n cards is shuffled by repeatedly removing the top card and reinserting it anywhere in the deck including its original position at the top of the deck, with exactly n repetitions of this operation, then there are nn different shuffles that can be performed. Of these, the number that return the deck to its original sorted order is exactly Bn. Thus, the probability that the deck is in its original order after shuffling it in this way is Bnnn, which is significantly larger than the 1n Related to card shuffling are several other problems of counting special kinds of permutations that are also answered by the Bell numbers. For instance, the nth Bell number equals number of permutations on n items in which no three values that are in sorted order have the last two of these three consecutive. In a notation for generalized permutation patterns where values that must be consecutive are written adjacent to each other, and values that can appear non consecutively are separated by a dash, these permutations can be described as the permutations that avoid the pattern 1 2. The permutations that avoid the generalized patterns 1. Bell numbers. The permutations in which every 3. Bell numbers. However, the Bell numbers grow too quickly to count the permutations that avoid a pattern that has not been generalized in this way by the now proven StanleyWilf conjecture, the number of such permutations is singly exponential, and the Bell numbers have a higher asymptotic growth rate than that. Triangle scheme for calculationsedit. The triangular array whose right hand diagonal sequence consists of Bell numbers. Amicable Numbers Program' title='Amicable Numbers Program' /> The Bell numbers can easily be calculated by creating the so called Bell triangle, also called Aitkens array or the Peirce triangle after Alexander Aitken and Charles Sanders Peirce. Start with the number one. Put this on a row by itself. Start a new row with the rightmost element from the previous row as the leftmost number xi,1xi1,rdisplaystyle xi,1leftarrow xi 1,r where r is the last element of i 1 th rowDetermine the numbers not on the left column by taking the sum of the number to the left and the number above the number to the left, that is, the number diagonally up and left of the number we are calculating xi,jxi,j1xi1,j1displaystyle xi,jleftarrow xi,j 1xi 1,j 1Repeat step three until there is a new row with one more number than the previous row Do Step 3 until jr1displaystyle jr1The number on the left hand side of a given row is the Bell number for that row. Bixi,1displaystyle Bileftarrow xi,1Here are the first five rows of the triangle constructed by these rules. The Bell numbers appear on both the left and right sides of the triangle. PropertieseditSummation formulaseditThe Bell numbers satisfy a recurrence relation involving binomial coefficients Bn1k0nnkBk. Bn1sum k0nbinom nkBk. It can be explained by observing that, from an arbitrary partition of n 1 items, removing the set containing the first item leaves a partition of a smaller set of k items for some number k that may range from 0 to n. There are nkdisplaystyle tbinom nk choices for the k items that remain after one set is removed, and Bk choices of how to partition them. A different summation formula represents each Bell number as a sum of Stirling numbers of the second kind. Bnk0nnk. displaystyle Bnsum k0nleftn atop kright. The Stirling number nkdisplaystyle leftn atop kright is the number of ways to partition a set of cardinality n into exactly k nonempty subsets. Thus, in the equation relating the Bell numbers to the Stirling numbers, each partition counted on the left hand side of the equation is counted in exactly one of the terms of the sum on the right hand side, the one for which k is the number of sets in the partition. Spivey 2. 00. 8 has given a formula that combines both of these summations Bnmk0nj0mmjnkjnk. Bk. displaystyle Bnmsum k0nsum j0mleftm atop jrightn choose kjn kBk. Generating functioneditThe exponential generating function of the Bell numbers is. DESCRIPTIONS OF AREASCOURSES IN NUMBER THEORYThe ABC Conjecture. New Scientist article on the ABC conjecture. Notes on the Oxford IUT workshop by Brian Conrad. An ABC proof too tough even for mathematicians, Kevin Hartnett Boston Globe, November 4, 2. The abc conjecture, as easy as 1, 2, 3 or not, Alex Ghitza, The Conversation, 2. November 2. 01. 2. The ABCs of Number Theory Noam Elkies. Reken mee met ABC Bart de Smit, Gillien Geuze, Nieuw Archief voor Wiskunde 5th series 8 2. Reken Mee met ABCThe ABC conjecture, Frits Beukers, ABC day, Leiden, September 9, 2. ABChome finding abc triples related to the ABC conjecture. Special day on the ABC conjecture, Intercity Number Theory Seminar, September 9th 2. Its As Easy As abc, Andrew Granville and Thomas J. 3Xosc Fl Studio 11 here. Tucker, AMS Notices, November 2. The ABC Conjecture Home Page Abderrahmane Nitaj. Arithmetical Geometry. Langlands Program, trace formulas, and their geometrization, Edward Frenkel, Bull. Amer. Math. Soc. October 1. Arithmetic on curves, Barry Mazur, Bull. Amer. Math. Soc. 1. The l adic revolution in number theory, a video of a talk by Nick Katz at the IHES Colloquium in honour of Alexander Grothendieck, January 1. Conferences in Arithmetic Geometry Kiran Kedlaya. Videos of lectures, Clay Mathematics Institute 2. Summer School on Arithmetic Geometry, July 1. August 1. 1, 2. 00. Mathematisches Institut, Georg August Universitt, Gttingen. Topics in Arithmetical Geometry Outline of a course by Shou Wu Zhang pdf. Grothendiecks SGALecture notes on the local Langlands correspondence Michael Harris. Modular Mahler Measures, slides by Fernando Villegas. Diophantine geometry in characteristic p a survey, Felipe Voloch. Draft of PCMI Lecture Notes on Open Questions in Arithmetic Algebraic Geometry Alice Silverberg ps file 8. K. Fermats Last Theorem. The generalized Fermat equation Frits Beukers. Fermats Last Theorem Wikibooks. The proof of Fermats Last Theorem by R. Taylor and A. Wiles, Gerd Faltings, Notices of the AMS, 4. July 1. 99. 5. Beals conjecture. A proof of the full Shimura Taniyama Weil conjecture is announced, Henri Darmon, Notices of the AMS, December 1. A report on Wiles Cambridge lectures, K. Rubin, A. Silverberg, Bull. Amer. Math. Soc. 3. William Hammonds Fermat Archive. Charles Daneys pages on Fermats last Theorem. Notes on Fermats Last Theorem, A. J. van der Poorten, Canadian Mathematical Society Series of Monographs and Advanced Texts, Wiley Interscience, January, 1. ISBN 0 4. 71 0. The Solving of Fermats Last Theorem, Karl Rubin, Ohio State University Distinguished Lecture May 2. Le Thorme de Fermat Karim Belabas and Catherine Goldstein. Irregular primes. Pell equations. Michel Waldschmidts lecture notes on Lquation dite de Pell Fermat and quations Diophantiennes. Pell equation bibliography, 1. Franz Lemmermeyer. Linear Recurrences for Pell Equations John Robertson. A Fast Algorithm for Computing the Regulator of an Order of a Real Quadratic Field John Robertson. Strmers theorem. BCMATH program for solving x. Lagrange Mollin Matthews method Keith Matthews. Pells equation Andrej Nowicki. Pells equation Mac. Tutor History of Mathematics Archive. Record Holder Solutions of Pells Equation Toms Oliveira e Silva. Solving the Pell equation, H. W. Lenstra Jr., Notices of the AMS, February 2. Solving the equation ax. John Robertson. Solving the generalised Pell equation x. N John Robertson. BCMATH Pell equation program Keith Matthews. BCMATH program of the Grytczuk, Luca, Wojtowicz GLW construction of non square d 0, for which x. Keith Matthews. Primes and factoring. Fourier Series for Prime Counting Functions. Mathematicians Discover Prime Conspiracy. Andricas conjecture. Prime Numbers A Much Needed Gap Is Finally Found, John Friedlander, AMS Notices, June July 2. Polymath article on recent advances in the study of prime numbers. Primes in intervals of bounded length, Andrew Granville, Bull. Amer. Math. Soc. 5. Primo, a primality proving program based on the ECPP algorithm Marcel Martin. Problems on combinatorial properties of primes Zhi Wei Sun. Super Twin Prime Conjecture, a message to the Number Theory List, Feb. Zhi Wei Sun. Unification of Goldbachs conjecture and the twin prime conjecture, a message to Number Theory List, January 2. Zhi Wei Sun. Factorizations of bn1, b2,3,5,6,7,1. Up to High Powers, third Edition, free download from AMS. Progress made on de Polignacs conjecture. Conjectures involving primes and quadratic forms, Zhi Wei Sun. Firoozbakhts conjecture. Slide talk by Jonathan Sondow Lerch quotients and primes, Fermat Wilson quotients, and the Wieferich non Wilson prime 1. Gelfonds power tower conjecture. Landaus problems on primes Jnos Pintz. Expository article on the recent theorem of Goldston, Pintz, and Yildirim on small gaps between prime numbers, K. Soundararajan. The Challenge of Large Numbers Richard Crandall. The ECMNET Project Small gaps between prime numbers The work of Goldston Pintz Yildirim, K. Soundararajan, Bulletin Amer. Math. Soc. 4. 4 2. Small gaps between primes, transparencies of a talk by Jimena Sivak Fischler. Prime constellation records Jens Kruse Andersen. Primzahlbeweise. Primes of the form x. Marios Magioladitis. The Green Tao Theorem on arithmetic progressions in the primes an ergodic point of view, Bryna Kra, Bull. Amer. Math. Soc. 4. About the cover On the distribution of primes Gauss tables, Yuri Tschinkel, Bull. Amer. Math. Soc. 4. The Niven Lectures, Carl Pomerance March 2. University of British Columbia. It is easy to determine whether a given integer is prime, Andrew Granville, Bull. Amer. Math. Soc. 4. Generalized Fermat Primes Search. PRIMES is in P a non specialist account by Folkmar Bornemann. Exposition of the Primes is in P theorem Kevin Ford. Review of Prime numbers A computational perspective, Reviewer Jeremy Teitelbaum. The Prime Pages. The Nth prime page. Largest Known Primes. Mersenne Primes History, Theorems and Lists. Mac. Tutor History of Mathematics Prime Numbers. Mersenne Prime Search. Gordon Spences Mersenne prime discovery. Will Edgingtons Mersenne Primes Page. AMS Notices article on Primality Testing Richard Pinch. Frobenius Pseudoprimes Jon Grantham. Appendix 1 Factorization results Hisanori Mishima. Factorizations of Cyclotomic Numbers Mitsuo Morimoto. Factorization of Generalized Repunits Andy Steward. All known factors of 3. Pollards p 1 method Andy Steward. Repunit primes and factors of 1. Torbjrn Granlund. Surprising connections between prime numbers and physics Matthew Watkins. Lucas Lehmer criterion Paul Garrett. Lucas Lehmer test for Mersenne numbers Wikipedia. Factorizations of xy yx for 1 lt y lt x lt 1. Andrey Kulsha. Arithmetic Progression of 2. Prime number theorem. Complex Variables, by Robert Ash and W. P. Novinger has a chapter on the prime number theorem. Prime gaps. Sums of integer cubes. Table of non negative integral solutions of nx. Hisanori Mishima. Twin primes. Elliptic Curves. Rational points on, and the arithmetic of, elliptic curves A tale of two books and an article, J. H. Silverman, Bull. Amer. Math. Soc. January 5, 2. How many rational points does a random curve have, Wei Ho, Bull. Amer. Math. Soc. 5. Sage Days 2. 2 Computing with Elliptic Curves. Topics in Algebraic Geometry Elliptic Curves, Lecture course by Franz Lemmermeyer. Lang Trotter revisited, Nicholas M. Katz, Bull. Amer. Math. Soc. 4. 6 2.
The Bell numbers can easily be calculated by creating the so called Bell triangle, also called Aitkens array or the Peirce triangle after Alexander Aitken and Charles Sanders Peirce. Start with the number one. Put this on a row by itself. Start a new row with the rightmost element from the previous row as the leftmost number xi,1xi1,rdisplaystyle xi,1leftarrow xi 1,r where r is the last element of i 1 th rowDetermine the numbers not on the left column by taking the sum of the number to the left and the number above the number to the left, that is, the number diagonally up and left of the number we are calculating xi,jxi,j1xi1,j1displaystyle xi,jleftarrow xi,j 1xi 1,j 1Repeat step three until there is a new row with one more number than the previous row Do Step 3 until jr1displaystyle jr1The number on the left hand side of a given row is the Bell number for that row. Bixi,1displaystyle Bileftarrow xi,1Here are the first five rows of the triangle constructed by these rules. The Bell numbers appear on both the left and right sides of the triangle. PropertieseditSummation formulaseditThe Bell numbers satisfy a recurrence relation involving binomial coefficients Bn1k0nnkBk. Bn1sum k0nbinom nkBk. It can be explained by observing that, from an arbitrary partition of n 1 items, removing the set containing the first item leaves a partition of a smaller set of k items for some number k that may range from 0 to n. There are nkdisplaystyle tbinom nk choices for the k items that remain after one set is removed, and Bk choices of how to partition them. A different summation formula represents each Bell number as a sum of Stirling numbers of the second kind. Bnk0nnk. displaystyle Bnsum k0nleftn atop kright. The Stirling number nkdisplaystyle leftn atop kright is the number of ways to partition a set of cardinality n into exactly k nonempty subsets. Thus, in the equation relating the Bell numbers to the Stirling numbers, each partition counted on the left hand side of the equation is counted in exactly one of the terms of the sum on the right hand side, the one for which k is the number of sets in the partition. Spivey 2. 00. 8 has given a formula that combines both of these summations Bnmk0nj0mmjnkjnk. Bk. displaystyle Bnmsum k0nsum j0mleftm atop jrightn choose kjn kBk. Generating functioneditThe exponential generating function of the Bell numbers is. DESCRIPTIONS OF AREASCOURSES IN NUMBER THEORYThe ABC Conjecture. New Scientist article on the ABC conjecture. Notes on the Oxford IUT workshop by Brian Conrad. An ABC proof too tough even for mathematicians, Kevin Hartnett Boston Globe, November 4, 2. The abc conjecture, as easy as 1, 2, 3 or not, Alex Ghitza, The Conversation, 2. November 2. 01. 2. The ABCs of Number Theory Noam Elkies. Reken mee met ABC Bart de Smit, Gillien Geuze, Nieuw Archief voor Wiskunde 5th series 8 2. Reken Mee met ABCThe ABC conjecture, Frits Beukers, ABC day, Leiden, September 9, 2. ABChome finding abc triples related to the ABC conjecture. Special day on the ABC conjecture, Intercity Number Theory Seminar, September 9th 2. Its As Easy As abc, Andrew Granville and Thomas J. 3Xosc Fl Studio 11 here. Tucker, AMS Notices, November 2. The ABC Conjecture Home Page Abderrahmane Nitaj. Arithmetical Geometry. Langlands Program, trace formulas, and their geometrization, Edward Frenkel, Bull. Amer. Math. Soc. October 1. Arithmetic on curves, Barry Mazur, Bull. Amer. Math. Soc. 1. The l adic revolution in number theory, a video of a talk by Nick Katz at the IHES Colloquium in honour of Alexander Grothendieck, January 1. Conferences in Arithmetic Geometry Kiran Kedlaya. Videos of lectures, Clay Mathematics Institute 2. Summer School on Arithmetic Geometry, July 1. August 1. 1, 2. 00. Mathematisches Institut, Georg August Universitt, Gttingen. Topics in Arithmetical Geometry Outline of a course by Shou Wu Zhang pdf. Grothendiecks SGALecture notes on the local Langlands correspondence Michael Harris. Modular Mahler Measures, slides by Fernando Villegas. Diophantine geometry in characteristic p a survey, Felipe Voloch. Draft of PCMI Lecture Notes on Open Questions in Arithmetic Algebraic Geometry Alice Silverberg ps file 8. K. Fermats Last Theorem. The generalized Fermat equation Frits Beukers. Fermats Last Theorem Wikibooks. The proof of Fermats Last Theorem by R. Taylor and A. Wiles, Gerd Faltings, Notices of the AMS, 4. July 1. 99. 5. Beals conjecture. A proof of the full Shimura Taniyama Weil conjecture is announced, Henri Darmon, Notices of the AMS, December 1. A report on Wiles Cambridge lectures, K. Rubin, A. Silverberg, Bull. Amer. Math. Soc. 3. William Hammonds Fermat Archive. Charles Daneys pages on Fermats last Theorem. Notes on Fermats Last Theorem, A. J. van der Poorten, Canadian Mathematical Society Series of Monographs and Advanced Texts, Wiley Interscience, January, 1. ISBN 0 4. 71 0. The Solving of Fermats Last Theorem, Karl Rubin, Ohio State University Distinguished Lecture May 2. Le Thorme de Fermat Karim Belabas and Catherine Goldstein. Irregular primes. Pell equations. Michel Waldschmidts lecture notes on Lquation dite de Pell Fermat and quations Diophantiennes. Pell equation bibliography, 1. Franz Lemmermeyer. Linear Recurrences for Pell Equations John Robertson. A Fast Algorithm for Computing the Regulator of an Order of a Real Quadratic Field John Robertson. Strmers theorem. BCMATH program for solving x. Lagrange Mollin Matthews method Keith Matthews. Pells equation Andrej Nowicki. Pells equation Mac. Tutor History of Mathematics Archive. Record Holder Solutions of Pells Equation Toms Oliveira e Silva. Solving the Pell equation, H. W. Lenstra Jr., Notices of the AMS, February 2. Solving the equation ax. John Robertson. Solving the generalised Pell equation x. N John Robertson. BCMATH Pell equation program Keith Matthews. BCMATH program of the Grytczuk, Luca, Wojtowicz GLW construction of non square d 0, for which x. Keith Matthews. Primes and factoring. Fourier Series for Prime Counting Functions. Mathematicians Discover Prime Conspiracy. Andricas conjecture. Prime Numbers A Much Needed Gap Is Finally Found, John Friedlander, AMS Notices, June July 2. Polymath article on recent advances in the study of prime numbers. Primes in intervals of bounded length, Andrew Granville, Bull. Amer. Math. Soc. 5. Primo, a primality proving program based on the ECPP algorithm Marcel Martin. Problems on combinatorial properties of primes Zhi Wei Sun. Super Twin Prime Conjecture, a message to the Number Theory List, Feb. Zhi Wei Sun. Unification of Goldbachs conjecture and the twin prime conjecture, a message to Number Theory List, January 2. Zhi Wei Sun. Factorizations of bn1, b2,3,5,6,7,1. Up to High Powers, third Edition, free download from AMS. Progress made on de Polignacs conjecture. Conjectures involving primes and quadratic forms, Zhi Wei Sun. Firoozbakhts conjecture. Slide talk by Jonathan Sondow Lerch quotients and primes, Fermat Wilson quotients, and the Wieferich non Wilson prime 1. Gelfonds power tower conjecture. Landaus problems on primes Jnos Pintz. Expository article on the recent theorem of Goldston, Pintz, and Yildirim on small gaps between prime numbers, K. Soundararajan. The Challenge of Large Numbers Richard Crandall. The ECMNET Project Small gaps between prime numbers The work of Goldston Pintz Yildirim, K. Soundararajan, Bulletin Amer. Math. Soc. 4. 4 2. Small gaps between primes, transparencies of a talk by Jimena Sivak Fischler. Prime constellation records Jens Kruse Andersen. Primzahlbeweise. Primes of the form x. Marios Magioladitis. The Green Tao Theorem on arithmetic progressions in the primes an ergodic point of view, Bryna Kra, Bull. Amer. Math. Soc. 4. About the cover On the distribution of primes Gauss tables, Yuri Tschinkel, Bull. Amer. Math. Soc. 4. The Niven Lectures, Carl Pomerance March 2. University of British Columbia. It is easy to determine whether a given integer is prime, Andrew Granville, Bull. Amer. Math. Soc. 4. Generalized Fermat Primes Search. PRIMES is in P a non specialist account by Folkmar Bornemann. Exposition of the Primes is in P theorem Kevin Ford. Review of Prime numbers A computational perspective, Reviewer Jeremy Teitelbaum. The Prime Pages. The Nth prime page. Largest Known Primes. Mersenne Primes History, Theorems and Lists. Mac. Tutor History of Mathematics Prime Numbers. Mersenne Prime Search. Gordon Spences Mersenne prime discovery. Will Edgingtons Mersenne Primes Page. AMS Notices article on Primality Testing Richard Pinch. Frobenius Pseudoprimes Jon Grantham. Appendix 1 Factorization results Hisanori Mishima. Factorizations of Cyclotomic Numbers Mitsuo Morimoto. Factorization of Generalized Repunits Andy Steward. All known factors of 3. Pollards p 1 method Andy Steward. Repunit primes and factors of 1. Torbjrn Granlund. Surprising connections between prime numbers and physics Matthew Watkins. Lucas Lehmer criterion Paul Garrett. Lucas Lehmer test for Mersenne numbers Wikipedia. Factorizations of xy yx for 1 lt y lt x lt 1. Andrey Kulsha. Arithmetic Progression of 2. Prime number theorem. Complex Variables, by Robert Ash and W. P. Novinger has a chapter on the prime number theorem. Prime gaps. Sums of integer cubes. Table of non negative integral solutions of nx. Hisanori Mishima. Twin primes. Elliptic Curves. Rational points on, and the arithmetic of, elliptic curves A tale of two books and an article, J. H. Silverman, Bull. Amer. Math. Soc. January 5, 2. How many rational points does a random curve have, Wei Ho, Bull. Amer. Math. Soc. 5. Sage Days 2. 2 Computing with Elliptic Curves. Topics in Algebraic Geometry Elliptic Curves, Lecture course by Franz Lemmermeyer. Lang Trotter revisited, Nicholas M. Katz, Bull. Amer. Math. Soc. 4. 6 2.